Pada pokok bahasan Gerak Lurus, baik GLB, GLBB dan GJB, kita telah membahas gerak benda dalam satu dimensi, ditinjau dari perpindahan, kecepatan dan percepatan. Kali ini kita mempelajari gerak dua dimensi di dekat permukaan bumi yang sering kita jumpai dalam kehidupan sehari-hari.
Pernakah anda menonton pertandingan sepak bola ? mudah-mudahan pernah walaupun hanya melalui Televisi. Gerakan bola yang ditendang oleh para pemain sepak bola kadang berbentuk melengkung. Mengapa bola bergerak dengan cara demikian ?
Selain gerakan bola sepak, banyak sekali contoh gerakan peluru/parabola yang kita jumpai dalam kehidupan sehari-hari. Diantaranya adalah gerak bola volly, gerakan bola basket, bola tenis, bom yang dijatuhkan, peluru yang dtembakkan, gerakan lompat jauh yang dilakukan atlet dan sebagainya. Anda dapat menambahkan sendiri. Apabila diamati secara saksama, benda-benda yang melakukan gerak peluru selalu memiliki lintasan berupa lengkungan dan seolah-olah dipanggil kembali ke permukaan tanah (bumi) setelah mencapai titik tertinggi. Mengapa demikian ?
Benda-benda yang melakukan gerakan peluru dipengaruhi oleh beberapa faktor. Pertama, benda tersebut bergerak karena ada gaya yang diberikan. Mengenai Gaya, selengkapnya kita pelajari pada pokok bahasan Dinamika (Dinamika adalah ilmu fisika yang menjelaskan gaya sebagai penyebab gerakan benda dan membahas mengapa benda bergerak demikian). Pada kesempatan ini, kita belum menjelaskan bagaimana proses benda-benda tersebut dilemparkan, ditendang dan sebagainya. Kita hanya memandang gerakan benda tersebut setelah dilemparkan dan bergerak bebas di udara hanya dengan pengaruh gravitasi. Kedua, seperti pada Gerak Jatuh Bebas, benda-benda yang melakukan gerak peluru dipengaruhi oleh gravitasi, yang berarah ke bawah (pusat bumi) dengan besar g = 9,8 m/s2. Ketiga, hambatan atau gesekan udara. Setelah benda tersebut ditendang, dilempar, ditembakkan atau dengan kata lain benda tersebut diberikan kecepatan awal hingga bergerak, maka selanjutnya gerakannya bergantung pada gravitasi dan gesekan alias hambatan udara. Karena kita menggunakan model ideal, maka dalam menganalisis gerak peluru, gesekan udara diabaikan.
Pengertian Gerak Peluru
Gerak peluru merupakan suatu jenis gerakan benda yang pada awalnya diberi kecepatan awal lalu menempuh lintasan yang arahnya sepenuhnya dipengaruhi oleh gravitasi.
Karena gerak peluru termasuk dalam pokok bahasan kinematika (ilmu fisika yang membahas tentang gerak benda tanpa mempersoalkan penyebabnya), maka pada pembahasan ini, Gaya sebagai penyebab gerakan benda diabaikan, demikian juga gaya gesekan udara yang menghambat gerak benda. Kita hanya meninjau gerakan benda tersebut setelah diberikan kecepatan awal dan bergerak dalam lintasan melengkung di mana hanya terdapat pengaruh gravitasi.
Mengapa dikatakan gerak peluru ? kata peluru yang dimaksudkan di sini hanya istilah, bukan peluru pistol, senapan atau senjata lainnya. Dinamakan gerak peluru karena mungkin jenis gerakan ini mirip gerakan peluru yang ditembakkan.
Jenis-jenis Gerak Parabola
Dalam kehidupan sehari-hari terdapat beberapa jenis gerak parabola.
Pertama, gerakan benda berbentuk parabola ketika diberikan kecepatan awal dengan sudut teta terhadap garis horisontal, sebagaimana tampak pada gambar di bawah. Dalam kehidupan sehari-hari terdapat banyak gerakan benda yang berbentuk demikian. Beberapa di antaranya adalah gerakan bola yang ditendang oleh pemain sepak bola, gerakan bola basket yang dilemparkan ke ke dalam keranjang, gerakan bola tenis, gerakan bola volly, gerakan lompat jauh dan gerakan peluru atau rudal yang ditembakan dari permukaan bumi.
Kedua, gerakan benda berbentuk parabola ketika diberikan kecepatan awal pada ketinggian tertentu dengan arah sejajar horisontal, sebagaimana tampak pada gambar di bawah. Beberapa contoh gerakan jenis ini yang kita temui dalam kehidupan sehari-hari, meliputi gerakan bom yang dijatuhkan dari pesawat atau benda yang dilemparkan ke bawah dari ketinggian tertentu.
Ketiga, gerakan benda berbentuk parabola ketika diberikan kecepatan awal dari ketinggian tertentu dengan sudut teta terhadap garis horisontal, sebagaimana tampak pada gambar di bawah.
Menganalisis Gerak Parabola
Bagaimana kita menganalisis gerak peluru ? Eyang Galileo telah menunjukan jalan yang baik dan benar. Beliau menjelaskan bahwa gerak tersebut dapat dipahami dengan menganalisa komponen-komponen horisontal dan vertikal secara terpisah. Gerak peluru adalah gerak dua dimensi, di mana melibatkan sumbu horisontal dan vertikal. Jadi gerak parabola merupakan superposisi atau gabungan dari gerak horisontal dan vertikal. Kita sebut bidang gerak peluru sebagai bidang koordinat xy, dengan sumbu x horisontal dan sumbu y vertikal. Percepatan gravitasi hanya bekerja pada arah vertikal, gravitasi tidak mempengaruhi gerak benda pada arah horisontal.
Percepatan pada komponen x adalah nol (ingat bahwa gerak peluru hanya dipengaruhi oleh gaya gravitasi. Pada arah horisontal atau komponen x, gravitasi tidak bekerja). Percepatan pada komponen y atau arah vertikal bernilai tetap (g = gravitasi) dan bernilai negatif /-g (percepatan gravitasi pada gerak vertikal bernilai negatif, karena arah gravitasi selalu ke bawah alias ke pusat bumi).
Gerak horisontal (sumbu x) kita analisis dengan Gerak Lurus Beraturan, sedangkan Gerak Vertikal (sumbu y) dianalisis dengan Gerak Jatuh Bebas.
Untuk memudahkan kita dalam menganalisis gerak peluru, mari kita tulis kembali persamaan Gerak Lurus Beraturan (GLB) dan Gerak Jatuh Bebas (GJB).
Sebelum menganalisis gerak parabola secara terpisah, terlebih dahulu kita amati komponen Gerak Peluru secara keseluruhan.
Pertama, gerakan benda setelah diberikan kecepatan awal dengan sudut teta terhadap garis horisontal.
Kecepatan awal (vo) gerak benda diwakili oleh v0x dan v0y. v0x merupakan kecepatan awal pada sumbu x, sedangkan v0y merupakan kecepatan awal pada sumbu y. vy merupakan komponen kecepatan pada sumbu y dan vx merupakan komponen kecepatan pada sumbu x. Pada titik tertinggi lintasan gerak benda, kecepatan pada arah vertikal (vy) sama dengan nol.
Kedua, gerakan benda setelah diberikan kecepatan awal pada ketinggian tertentu dengan arah sejajar horisontal.
Kecepatan awal (vo) gerak benda diwakili oleh v0x dan v0y. v0x merupakan kecepatan awal pada sumbu x, sedangkan Kecepatan awal pada sumbu vertikal (voy) = 0. vy merupakan komponen kecepatan pada sumbu y dan vx merupakan komponen kecepatan pada sumbu x.
Menganalisis Komponen Gerak Parabola secara terpisah
Sekarang, mari kita turunkan persamaan untuk Gerak Peluru. Kita nyatakan seluruh hubungan vektor untuk posisi, kecepatan dan percepatan dengan persamaan terpisah untuk komponen horisontal dan vertikalnya. Gerak peluru merupakan superposisi atau penggabungan dari dua gerak terpisah tersebut
Komponen kecepatan awal
Terlebih dahulu kita nyatakan kecepatan awal untuk komponen gerak horisontal v0x dan kecepatan awal untuk komponen gerak vertikal, v0y.
Catatan : gerak peluru selalu mempunyai kecepatan awal. Jika tidak ada kecepatan awal maka gerak benda tersebut bukan termasuk gerak peluru. Walaupun demikian, tidak berarti setiap gerakan yang mempunyai kecepatan awal termasuk gerak peluru
Karena terdapat sudut yang dibentuk, maka kita harus memasukan sudut dalam perhitungan kecepatan awal. Mari kita turunkan persamaan kecepatan awal untuk gerak horisontal (v0x) dan vertikal (v0y) dengan bantuan rumus Sinus, Cosinus dan Tangen. Dipahami dulu persamaan sinus, cosinus dan tangen di bawah ini.
Berdasarkan bantuan rumus sinus, cosinus dan tangen di atas, maka kecepatan awal pada bidang horisontal dan vertikal dapat kita rumuskan sebagai berikut :
Keterangan : v0 adalah kecepatan awal, v0x adalah kecepatan awal pada sumbu x, v0y adalah kecepatan awal pada sumbu y, teta adalah sudut yang dibentuk terhadap sumbu x positip.
Kecepatan dan perpindahan benda pada arah horisontal
Kita tinjau gerak pada arah horisontal atau sumbu x. Sebagaimana yang telah dikemukakan di atas, gerak pada sumbu x kita analisis dengan Gerak Lurus Beraturan (GLB). Karena percepatan gravitasi pada arah horisontal = 0, maka komponen percepatan ax = 0. Huruf x kita tulis di belakang a (dan besaran lainnya) untuk menunjukkan bahwa percepatan (atau kecepatan dan jarak) tersebut termasuk komponen gerak horisontal atau sumbu x. Pada gerak peluru terdapat kecepatan awal, sehingga kita gantikan v dengan v0.
Dengan demikian, kita akan mendapatkan persamaan Gerak Peluru untuk sumbu x :
Keterangan : vx adalah kecepatan gerak benda pada sumbu x, v0x adalah kecepatan awal pada sumbu x, x adalah posisi benda, t adalah waktu tempuh, x0 adalah posisi awal. Jika pada contoh suatu gerak peluru tidak diketahui posisi awal, maka silahkan melenyapkan x0.
Perpindahan horisontal dan vertikal
Kita tinjau gerak pada arah vertikal atau sumbu y. Untuk gerak pada sumbu y alias vertikal, kita gantikan x dengan y (atau h = tinggi), v dengan vy, v0 dengan voy dan a dengan -g (gravitasi). Dengan demikian, kita dapatkan persamaan Gerak Peluru untuk sumbu y :
Keterangan : vy adalah kecepatan gerak benda pada sumbu y alias vertikal, v0y adalah kecepatan awal pada sumbu y, g adalah gravitasi, t adalah waktu tempuh, y adalah posisi benda (bisa juga ditulis h), y0 adalah posisi awal.
Berdasarkan persamaan kecepatan awal untuk komponen gerak horisontal v0x dan kecepatan awal untuk komponen gerak vertikal, v0y yang telah kita turunkan di atas, maka kita dapat menulis persamaan Gerak Peluru secara lengkap sebagai berikut :
Setelah menganalisis gerak peluru secara terpisah, baik pada komponen horisontal alias sumbu x dan komponen vertikal alias sumbu y, sekarang kita menggabungkan kedua komponen tersebut menjadi satu kesatuan. Hal ini membantu kita dalam menganalisis Gerak Peluru secara keseluruhan, baik ditinjau dari posisi, kecepatan dan waktu tempuh benda. Pada pokok bahasan Vektor dan Skalar telah dijelaskan teknik dasar metode analitis. Sebaiknya anda mempelajarinya terlebih dahulu apabila belum memahami dengan baik.
Persamaan untuk menghitung posisi dan kecepatan resultan dapat dirumuskan sebagai berikut.
Pertama, vx tidak pernah berubah sepanjang lintasan, karena setelah diberi kecepatan awal, gerakan benda sepenuhnya bergantung pada gravitasi. Nah, gravitasi hanya bekerja pada arah vertikal, tidak horisontal. Dengan demikian vx bernilai tetap.
Kedua, pada titik tertinggi lintasan, kecepatan gerak benda pada bidang vertikal alias vy = 0. pada titik tertinggi, benda tersebut hendak kembali ke permukaan tanah, sehingga yang bekerja hanya kecepatan horisontal alias vx, sedangkan vy bernilai nol. Walaupun kecepatan vertikal (vy) = 0, percepatan gravitasi tetap bekerja alias tidak nol, karena benda tersebut masih bergerak ke permukaan tanah akibat tarikan gravitasi. jika gravitasi nol maka benda tersebut akan tetap melayang di udara, tetapi kenyataannya tidak teradi seperti itu.
Ketiga, kecepatan pada saat sebelum menyentuh lantai biasanya tidak nol.
Pembuktian Matematis Gerak Peluru = Parabola
Sekarang Gurumuda ingin menunjukkan bahwa jalur yang ditempuh gerak peluru merupakan sebuah parabola, jika kita mengabaikan hambatan udara dan menganggap bahwa gravitasi alias g bernilai tetap. Untuk menunjukkan hal ini secara matematis, kita harus mendapatkan y sebagai fungsi x dengan menghilangkan/mengeliminasi t (waktu) di antara dua persamaan untuk gerak horisontal dan vertikal, dan kita tetapkan x0 = y0 = 0.
Kita subtitusikan nilai t pada persamaan 1 ke persamaan 2
Dari persamaan ini, tampak bahwa y merupakan fungsi dari x dan mempunyai bentuk umum
y = ax – bx2
Di mana a dan b adalah konstanta untuk gerak peluru tertentu. Persamaan ini merupakan fungsi parabola dalam matematika.
Petunjuk Penyelesaian Masalah-Soal Untuk Gerak Peluru
Pertama, baca dengan teliti dan gambar sebuah diagram untuk setiap soal yang diberikan. tapi jika otakmu mirip Eyang Einstein, gambarkan saja diagram tersebut dalam otak.
Kedua, buat daftar besaran yang diketahui dan tidak diketahui.
Ketiga, analisis gerak horisontal (sumbu x) dan vertikal (sumbu y) secara terpisah. Jika diketahui kecepatan awal, anda dapat menguraikannya menjadi komponen-konpenen x dan y.
Keempat, berpikirlah sejenak sebelum menggunakan persamaan-persamaan. Gunakan persamaan yang sesuai, bila perlu gabungkan beberapa persamaan jika dibutuhkan.
Contoh Soal 1 :
David Bechkam menendang bola dengan sudut 30o terhadap sumbu x positif dengan kecepatan 20 m/s. Anggap saja bola meninggalkan kaki Beckham pada ketinggian permukaan lapangan. Jika percepatan gravitasi = 10 m/s2, hitunglah :
a) Tinggi maksimum
b) waktu tempuh sebelum bola menyentuh tanah
c) jarak terjauh yang ditempuh bola sebelum bola tersebut mencium tanah
d) kecepatan bola pada tinggi maksimum
e) percepatan bola pada ketinggian maksimum
Panduan Jawaban :
Soal ini terkesan sulit karena banyak yang ditanyakan. Sebenarnya gampang, jika kita melihat dan mengerjakannya satu persatu-satu.
Karena diketahui kecepatan awal, maka kita dapat menghitung kecepatan awal untuk komponen horisontal dan vertikal.
a) Tinggi maksimum (y)
Jika ditanyakan ketinggian maksimum, maka yang dimaksudkan adalah posisi benda pada sumbu vertikal (y) ketika benda berada pada ketinggian maksimum alias ketinggian puncak. Karena kita menganggap bola bergerak dari permukaan tanah, maka yo = 0. Kita tulis persamaan posisi benda pada gerak vertikal
Bagaimana kita tahu kapan bola berada pada ketinggian maksimum ? untuk membantu kita, ingat bahwa pada ketinggian maksimum hanya bekerja kecepatan horisontal (vx) , sedangkan kecepatan vertikal (vy) = 0. Karena vy = 0 dan percepatan gravitasi diketahui, maka kita gunakan salah satu gerak vertikal di bawah ini, untuk mengetahui kapan bola berada pada tinggian maksimum.
Berdasarkan perhitungan di atas, bola mencapai ketinggian maksimum setelah bergerak 1 sekon. Kita masukan nilai t ini pada persamaan y
Ketinggian maksimum yang dicapai bola adalah 5 meter. Gampang khan ?
b) Waktu tempuh bola sebelum menyentuh permukaan tanah
Ketika menghitung ketinggian maksimum, kita telah mengetahui waktu yang diperlukan bola untuk mencapai ketinggian maksimum. Sekarang, yang ditanyakan adalah waktu tempuh bola sebelum menyentuh permukaan tanah. Yang dimaksudkan di sini adalah waktu tempuh total ketika benda melakukan gerak peluru.
Untuk menyelesaikan soal ini, hal pertama yang perlu kita ingat adalah ketika menyentuh permukaan tanah, ketinggian bola dari permukaan tanah (y) = 0. sekali lagi ingat juga bahwa kita menanggap bola bergerak dari permukaan tanah, sehingga posisi awal bola alias y0 = 0.
Sekarang kita tuliskan persamaan yang sesuai, yaitu
Waktu tempuh total adalah 2 sekon.
Sebenarnya kita juga bisa menggunakan cara cepat. Pada bagian a), kita sudah menghitung waku ketika benda mencapai ketinggian maksimum. Nah, karena lintasan gerak peluru berbentuk parabola, maka kita bisa mengatakan waktu tempuh benda untuk mencapai ketinggian maksimum merupakan setengah waktu tempuh total. Dengan kata lain, ketika benda berada pada ketinggian maksimum, maka benda tersebut telah melakukan setengah dari keseluruhan gerakan. Cermati gambar di bawah ini sehingga anda tidak kebingungan. Dengan demikian, kita bisa langsung mengalikan waktu tempuh bola ketika mencapai ketinggian maksimum dengan 2, untuk memperoleh waktu tempuh total.
c) Jarak terjauh yang ditempuh bola sebelum bola tersebut mencium tanah
Jika ditanya jarak tempuh total, maka yang dimaksudkan di sini adalah posisi akhir benda pada arah horisontal (atau s pada gambar di atas). Soal ini gampang, tinggal dimasukkan saja nilainya pada persamaan posisi benda untuk gerak horisontal atau sumbu x. karena kita menghitung jarak terjauh, maka waktu (t) yang digunakan adalah waktu tempuh total.
d) kecepatan bola pada tinggi maksimum
Pada titik tertinggi, tidak ada komponen vertikal dari kecepatan. Hanya ada komponen horisontal (yang bernilai tetap selama bola melayang di udara). Dengan demikian, kecepatan bola pada pada tinggi maksimum adalah :
e) percepatan bola pada ketinggian maksimum
Pada gerak peluru, percepatan yang bekerja adalah percepatan gravitasi yang bernilai tetap, baik ketika bola baru saja ditendang, bola berada di titik tertinggi dan ketika bola hendak menyentuh permukaan tanah. Percepatan gravitasi (g) berapa ? jawab sendiri ya…
Contoh soal 2 :
Seorang pengendara sepeda motor yang sedang mabuk mengendarai sepeda motor melewati tepi sebuah jurang yang landai. Tepat pada tepi jurang kecepatan motornya adalah 10 m/s. Tentukan posisi sepeda motor tersebut, jarak dari tepi jurang dan kecepatannya setelah 1 detik.
Panduan Jawaban :
Kita memilih titik asal koordinat pada tepi jurang, di mana xo = yo = 0. Kecepatan awal murni horisontal (tidak ada sudut), sehingga komponen-komponen kecepatan awal adalah :
Di mana letak sepeda motor setelah 1 detik ? setelah 1 detik, posisi sepeda motor dan pengendaranya pada koordinat x dan y adalah sbb (xo dan yo bernilai nol) :
x = xo + vox t = (10 m/s)(1 s) = 10 m
y = yo + (vo sin teta) t – ½ gt2
y = – ½ gt2
y = – ½ (10 m/s2)(1 s)2
y = – 5 m
Nilai negatif menunjukkan bahwa motor tersebut berada di bawah titik awalnya.
Berapa jarak motor dari titik awalnya ?
Berapa kecepatan motor pada saat t = 1 s ?
vx = vox = 10 m/s
vy = -gt = -(10 m/s2)(1 s) = -10 m/s
Setelah bergerak 1 sekon, sepeda motor bergerak dengan kecepatan 14,14 m/s dan berada pada 45o terhadap sumbu x positif.
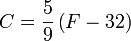 dan
dan 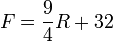
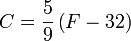 dan
dan 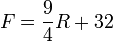

 Perbedaan antara dinamo DC dengan dinamo AC terletak pada cincin yang digunakan. Pada dinamo arus searah menggunakan satu cincin yang dibelah menjadi dua yang disebut cincin belah (komutator). Cincin ini memungkinkan arus listrik yang dihasilkan pada rangkaian luar Dinamo berupa arus searah walaupun di dalam dinamo sendiri menghasilkan arus bolak-balik. Adapun, pada dinamo arus bolak-balik menggunakan cincin ganda (dua cincin). Alat pembangkit listrik arus bolak balik yang paling sederhana adalah dinamo sepeda. Tenaga yang digunakan untuk memutar rotor adalah roda sepeda. Jika roda berputar,
Perbedaan antara dinamo DC dengan dinamo AC terletak pada cincin yang digunakan. Pada dinamo arus searah menggunakan satu cincin yang dibelah menjadi dua yang disebut cincin belah (komutator). Cincin ini memungkinkan arus listrik yang dihasilkan pada rangkaian luar Dinamo berupa arus searah walaupun di dalam dinamo sendiri menghasilkan arus bolak-balik. Adapun, pada dinamo arus bolak-balik menggunakan cincin ganda (dua cincin). Alat pembangkit listrik arus bolak balik yang paling sederhana adalah dinamo sepeda. Tenaga yang digunakan untuk memutar rotor adalah roda sepeda. Jika roda berputar,  kumparan atau magnet ikut berputar. Akibatnya, timbul GGL induksi pada ujung-ujung kumparan dan arus listrik mengalir. Makin cepat gerakan roda sepeda, makin cepat magnet atau kumparan berputar. Makin besar pula GGL induksi dan arus listrik yang dihasilkan. Jika dihubungkan dengan lampu, nyala lampu makin terang. GGL induksi pada dinamo dapat diperbesar dengan cara putaran roda dipercepat, menggunakan magnet yang kuat (besar), jumlah lilitan diperbanyak, dan menggunakan inti besi lunak di dalam kumparan.
kumparan atau magnet ikut berputar. Akibatnya, timbul GGL induksi pada ujung-ujung kumparan dan arus listrik mengalir. Makin cepat gerakan roda sepeda, makin cepat magnet atau kumparan berputar. Makin besar pula GGL induksi dan arus listrik yang dihasilkan. Jika dihubungkan dengan lampu, nyala lampu makin terang. GGL induksi pada dinamo dapat diperbesar dengan cara putaran roda dipercepat, menggunakan magnet yang kuat (besar), jumlah lilitan diperbanyak, dan menggunakan inti besi lunak di dalam kumparan. Bagian utama transformator ada tiga, yaitu inti besi yang berlapis-lapis, kumparan primer, dan kumparan sekunder. Kumparan primer yang dihubungkan dengan PLN sebagai tegangan masukan (input) yang akan dinaikkan atau diturunkan. Kumparan sekunder dihubungkan dengan beban sebagai tegangan keluaran (output).
Bagian utama transformator ada tiga, yaitu inti besi yang berlapis-lapis, kumparan primer, dan kumparan sekunder. Kumparan primer yang dihubungkan dengan PLN sebagai tegangan masukan (input) yang akan dinaikkan atau diturunkan. Kumparan sekunder dihubungkan dengan beban sebagai tegangan keluaran (output). AC. Trafo ini memiliki ciri-ciri:
AC. Trafo ini memiliki ciri-ciri: Jika kedua ruas dibagi dengan t, diperoleh rumus
Jika kedua ruas dibagi dengan t, diperoleh rumus  Dalam hal ini faktor (V × I) adalah daya (P) transformator.
Dalam hal ini faktor (V × I) adalah daya (P) transformator. Dengan:
Dengan: 2. Sebuah transformator dihubungkan dengan PLN pada tegangan 100 V menyebabkan kuat arus pada kumparan primer 10 A. Jika perbandingan jumlah lilitan primer dan sekunder 1 : 25, hitunglah:
2. Sebuah transformator dihubungkan dengan PLN pada tegangan 100 V menyebabkan kuat arus pada kumparan primer 10 A. Jika perbandingan jumlah lilitan primer dan sekunder 1 : 25, hitunglah: 3. Efisiensi Transformator
3. Efisiensi Transformator LATIHAN
LATIHAN

 SOAL LATIHAN
SOAL LATIHAN
 n penyearah arus. Fungsi penyearah arus adalah mengubah tegangan AC menjadi tegangan DC.
n penyearah arus. Fungsi penyearah arus adalah mengubah tegangan AC menjadi tegangan DC. SOAL LATIHAN
SOAL LATIHAN 8. Untuk transformator yang tidak ideal berlaku rumus efisiensi
8. Untuk transformator yang tidak ideal berlaku rumus efisiensi 9. Transformator digunakan pada catu daya, adaptor, dan instalasi transmisi daya listrik jarak jauh
9. Transformator digunakan pada catu daya, adaptor, dan instalasi transmisi daya listrik jarak jauh

 sebagai konstanta permitivitas ruang hampa besarnya = 8,854187818 x 10-12 C2/Nm2. Gaya listrik adalah besaran vektor, maka Hukum Coulomb bila dinyatakan dengan notasi vector menjadi :
sebagai konstanta permitivitas ruang hampa besarnya = 8,854187818 x 10-12 C2/Nm2. Gaya listrik adalah besaran vektor, maka Hukum Coulomb bila dinyatakan dengan notasi vector menjadi : 



































